Getting Started - Some Simple Programming Tasks
Below, we explore some basic Python programs using concepts from this week's class. These examples are inteded to demonstrate basic programming concepts, working with the Python development environment, and using variables in programs.
We also introduce numpy and matplotlib, two widely used Python packages. numpy provides a host of mathematical functions and array/matrix operations, and is used in most science and engineering applications written in Python. Complete documentation for numpy is available at https://numpy.org/. matplotlib is a simple, yet powerful, plotting/charting package for visualizing data. Complete documentation for matplotlib is available at https://matplotlib.org. Both packages are open source and freely available.
Hello, World!
Our first program is very simple, and involves printing the string "Hello World" to the Python console.
Programming concepts demonstrated:
- Interacting with the Python environment
- using the "string" data type
- console output
print( "Hello, World!")
Compute the Trajectory of a Ball using the Laws of Motion
This problem involves computing a vertacal position (height) of a thrown ball based on the laws of motion. These laws are:
$\large h = h_0 + v_0 t - \frac{1}{2} g t^2 $
$\large v = v_0 - g t $
where: $ g = 9.8 \frac{m}{s^2} $, the acceleration due to gravity.
We want to compute, for a given time t, the position and speed of the ball at that point in time. Assume the following intial conditions:
$ h_0 = 1.2 m $ $ v_0 = 5.4 m/s $
Calculate your results for t = 0.5 seconds, and t=2 seconds.
The Strategy
To compute this trajectory, we employ the following strategy:
Define a function capturing the Laws of Motion above. This function will take as input the following:
- a time variable (
t) indicating the point in time to evaluate, - the initial position (height) of the ball (
h0) the initial velocity (in the vertical direction) of the ball (
v0)The function should return the position and velocity for the given input above.
- a time variable (
Call this function to determine the position and velocities for the two times given above.
Report the results.
Note the use of comments to document your code - any text to the right of a '#' symbol is considered a comment and is ignored by the Python interpreter. Use comments liberally throughout your program to indicate variable meanings, program logic, and other aspects of your program in "human-friendly", readable forms. You will thank yourself when you look at your code a few weeks from now and have to remember what you did.
For most engineering problems, units are critical to your calculations. It is very helpful, and will save you a lot of headaches trying to debug faulty code, to indicate units associated with your variables and calculations in comments at the point of definition.
When printing your output, we use appropriate formatting! e.g. for floating point (real) numbers, indicate a precision using string formatting, e.g.
print( "My Output is: {}, {:.2f}".format(someInteger, someRealNumber) )
# Program for calculating hieght and velocity of a ball thrown vertically in the air
# first, define function that computes position, velocity
# t = time to evaluate
# h0 = initial height
# v0 = initial vertical velocity
def LawOfMotion(t,h0,v0):
g = 9.8 # m/s/s
# calculate height
h = h0 + (v0*time) - 0.5*g*time**2 # m
# calculate velocity
v = v0 - g*time # m/s
return h,v # return both h and v to the caller
# ----- main program -----
# define initial conditions, constants
h0 = 1.2 # meters
v0 = 5.4 # m/s
time = 0.5 # second
h,v = LawOfMotion(time,h0,v0)
print ( "After {} seconds, Velocity={:.2f}m/s, Height={:.2}m".format( time, v, h))
# repeat, getting values after two seconds
time = 2
h,v = LawOfMotion(time,h0,v0)
print ( "After {} seconds, Velocity={:.2f}m/s, Height={:.2f}m".format( time, v, h))
Using Numpy and Matplotlib
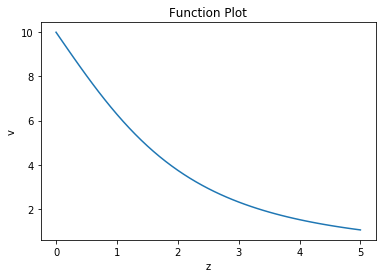
The next program evaluates a complex mathematical function for multiple input values. We employ numpy for two reasons: 1) t make an array of input values, and 2) to use numpys sqrt() function, which accepts both a single value and arrays of input values when evaluating a mathematival function. When we pass an single input value, we get a single result; when we provide an array of input values, numpys math function will return a corresponding array of results. This powerful capability allows us to write short programs that compute entire arrays of results.
The mathematical function we want to evaluate is:
$ V = V_0 \left(1-\large \frac{z}{\sqrt{a^2+z^2}}\right) $
for:
$ V_0 = 10 $
$ a = 2.5$
We want to evaluate this function for z in the range [0,5]. We also want to see a plot of this function over the specified range.
The Strategy
- Create a set of input values for z.
- Using this input array, calculate the corresponding function values, remebering the resulting array
- Plot the results vs. our input (z) values
import numpy as np # np is an 'alias' for numpy
import matplotlib.pyplot as plt # plt is an 'alias' for numpy
# use numpy to create a range of z values, starting at
z = np.arange(0,5.01,0.1) # array starts at zero, goes up to (but not including) 5.01, so last value is 5.0
# declare additional input variables
v0 = 10
a = 2.5
# solve function (note that since 'z' is an array, an array of results 'v' is returned
v = v0*(1-(z/((a**2 + z**2)**0.5)))
plt.plot(z,v) # add a trace to the plot
plt.xlabel('z') # set x and y labels
plt.ylabel('v')
plt.title("Function Plot")
plt.show() # show the plot